Matcom Online Grader

Serán dados n rectángulos numerados desde 1 hasta n. Nosotros los ubicaremos sobre el eje OX , de izquierda a derecha, acorde a los números de los rectángulos. Cada rectángulo permanece sobre el eje OX por su lado más corto o por su lado más largo ( ver la figura de abajo ). Calcule la longitud de la línea que los envuelve superiormente, es decir, la longitud del perímetro de la figura obtenida menos la longitud del segmento de la  línea vertical de la izquierda, la derecha y la parte de abajo de la figura. Escriba un programa para encontrar la máxima longitud posible de la línea envolvente superior.

Input

En la primera línea de la entrada estándar, el valor de n. En cada una de las siguientes n líneas, dos enteros son dados – ai y  bi – la longitudes de los lados del i-ésimo rectángulo.

Restricciones : 1 <= n <= 1000; 1 <= ai <= bi <= 1000, para cada i = 1, 2,…, n.

Output

En una línea de la salida estándar, su programa debe  escribir el resultado  como un entero positivo.

Sample test(s)

Hints

Hints
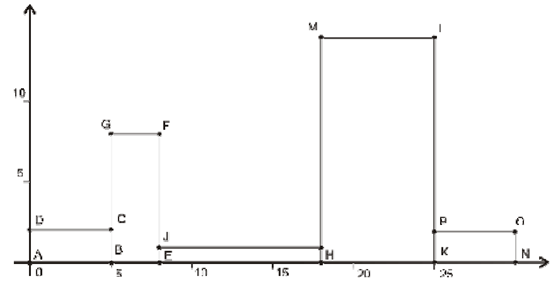
Una configuración, que produce la longitud máxima de la envoltura superior está representada en la figura. La línea de  la envoltura superior consiste de los segmentos DC, CG, GF, FJ, JI, IM, ML, LP, y PO. La longitud total es 5 + 6 + 3 + 7 + 10 + 13 + 7 + 12 +5 = 68.