Matcom Online Grader

La red de "autopistas con impuesto" en Byteland está creciendo muy rápidamente. Se ha convertido en tan densa que decidir la mejor ruta es un verdadero problema. La red está compuesta por autopistas bidireccionales que conectan ciudades. De cada autopista se conoce el tiempo necesario para recorrerla y el impuesto a pagar.
Una ruta está compuesta por autopistas consecutivas. El tiempo total necesario para recorrer una ruta es igual a la suma de los tiempos necesarios para recorrer cada autopista que la compone. Mientras más rápida y más barata, mejor es la ruta. Precisamente, una ruta es mejor que otra si se puede recorrer más rápido y no es más cara que la otra, o viceversa: si se puede pagar menos y no recorrerla más lento que la otra. Llamaremos mínima a una ruta que conecta a dos ciudades si no existe otra ruta mejor que conecta a esas dos ciudades. Desafortunadamente no siempre existe una ruta mínima entre dos ciudades: pueden existir varias rutas no comparables entre sí, o puede incluso no existir ninguna ruta.

La imagen de abajo muestra un ejemplo de red de autopistas. Cada autopista está marcada por un par de números: el impuesto y el tiempo de recorrido

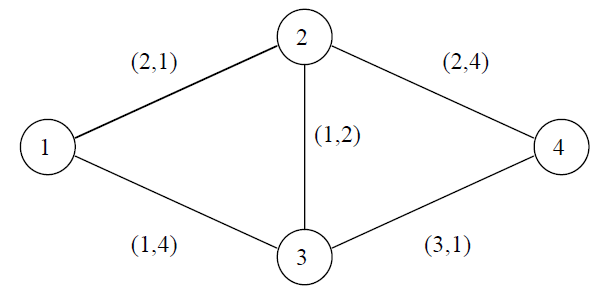
Consideremos cuatro rutas distintas desde la ciudad 1 a la 4, junto con sus impuestos y sus tiempos de recorrido:
1-2-3 (impuesto 4, tiempo 5)
1-3-4 (impuesto 4, tiempo 5)
1-2-3-4 (impuesto 6, tiempo 4)
1-3-2-4 (impuesto 4, tiempo 10)
Las rutas 1-3-4 y 1-2-4 son mejores que la 1-3-2-4. Hay dos pares impuesto-tiempo mínimos: impuesto 4, tiempo 5 (rutas 1-2-4 y 1-3-4) e impuesto 6, tiempo 4 (ruta 1-2-3-4). Al escoger la ruta debemos decidir si preferimos viajar más rápido pero con un mayor costo (ruta 1-2-3-4), o viajar más lento pero a un menos precio (ruta 1-3-4 o 1-2-4)

Tarea:
Tu tarea es escribir un programa que:
- Lea la descripción de la red de autopistas y las ciudades inicial y final de la ruta
- Calcule el número de rutas mínimas diferentes que conectan a la ciudades inicial y final, contando a todas las rutas con el mismo costo y tiempo de recorrido como una sola, estamos interesados solamente en el número de pares mínimos diferentes costo-tiempo.
- Imprima el resultado.

Input

Línea 1 : Cuatro enteros $N$, $M$, $S$, $E$ separados por un único espacio: la cantidad de ciudades $(1 \le N \le 100)$, el número de autopistas $(0 \le M \le 300)$, la ciudad inicial y la ciudad final de la ruta $(1 \le S, E \le N, S \ne E)$.
Línea 2 ... M+1 : Las próximas $M$ líneas describen a las autopistas, una por línea. Cada una de estas líneas contiene cuatro enteros separados por un único espacio: los dos extremos $p$ y $r$ de la autopista $(1 \le p, r \le n, p \ne r)$ el costo $c$ $(0 \le c \le 100)$ y el tiempo necesario para recorrerla $t$ $(0 \le t \le 100)$. Dos ciudades pueden estar conectadas por más de una autopista.

Output

Línea 1 : El número de pares mínimos diferentes costo-tiempo para rutas desde $S$ hasta $E$.

Sample test(s)