Matcom Online Grader
MOG Round #28Ended |
B - Intersección de rectángulos
Languages: C, C++, Java, Pascal, Haskell, Python, JavaScript, Tiger, C#
Time & Memory limits: (details)
Dado un conjunto de rectángulos $\{R_1, R_2, ..., R_n\}$, calcule el área de la intersección. Es decir:
$(R_1 \cap R_2 \cap ... \cap R_n)$.
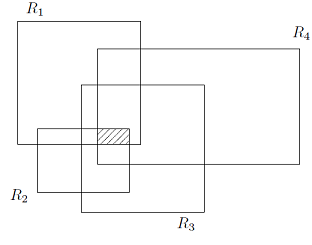
Los lados de los rectángulos $R_1, R_2, ..., R_n$ son líneas horizontales o verticales. Por ejemplo, la intersección de los cuatro rectángulos $R_1, R_2, R_3, R_4$ en la siguiente figura es el área sombreada:
Input
Línea 1
: Un entero $N$ $(1 \le N \le 1000)$ la cantidad de rectángulos.
Línea 2…N+1
: Cada una de las siguientes líneas contiene cuatro enteros $x_1, x_2, y_1, y_2$ $(0 \le x_1 \lt x_2 \le 10000, 0 \le y_1 \lt y_2 \le 10000)$ indicando que el rectángulo descrito está limitado por las rectas $x = x_1, x = x_2, y = y_1, y = y_2$
Output
Línea 1 : Un entero no negativo, el área de la intersección de los $N$ rectángulos.