Matcom Online Grader

Fito le compró a su novia Ana un collar. El collar está compuesto de $N$ perlas donde cada una está numerada con un entero diferente entre $1$ y $N$. Con la intención de hacer el regalo por todo lo alto, Fito decidió reordenar las perlas de forma tal que maximice la belleza del collar. La belleza del collar se define como la suma de la multiplicación de los números en perlas adyacentes. Por ejemplo, si $N=5$ la mejor forma de ubicar las perlas se muestra en la siguiente figura:

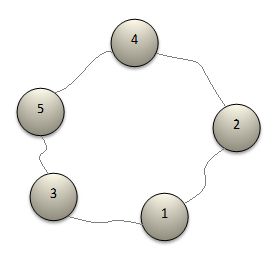
Nota que el valor de belleza del collar anterior es $1∗2+2∗4+4∗5+5∗3+3∗1=48$, y $48$ es en efecto el mayor valor de belleza que puede tomar un collar con $5$ perlas. Como la cantidad de perlas puede ser demasiado grande, Fito solamente te ha pedido que calcules el mayor valor de belleza que se puede obtener reordenando las $N$ perlas del collar.