Matcom Online Grader
Faculty of Mathematics and Computer Science of University of Havana

El juego del DOTA se juega en un mapa como este:

A pesar de todas las versiones que se han hecho de este juego, aún no se ha cambiado la estructura del mapa, así que Fito el mejor jugador de DOTA de nuestra facultad decidió hacer un concurso para construir nuevos mapas.

Como el mapa es simétrico respecto a la diagonal que va de izquierda a derecha, a Fito solo le interesa construir la mitad del mapa, y además le interesa que sea un árbol .

Un árbol es un grafo conexo tal que para todo par de vértices se cumple que hay un único camino, que no repita vértices, entre ellos.

Para poder hacer el concurso Fito necesita un algoritmo que determine si dos árboles son iguales, para de esta forma evitar que los concursantes hagan fraude. Los concursantes para entregar su árbol lo hacen de la siguiente forma:

1. A cada vértice le asignan un número.
2. Apuntan todas las parejas de números que le corresponden a nodos que tienen una arista entre ellos.

Por ejemplo si dos estudiantes entregan los siguientes árboles:

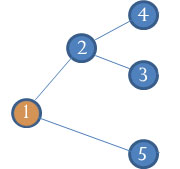
1 2 1 5 2 3 2 4

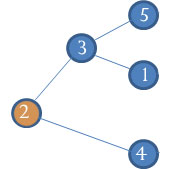
2 3 3 5 3 1 2 4

Ambos representaron el mismo árbol:

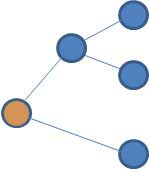
Fomalmente se puede definir que dos representaciones de árboles son iguales si existe una transformación de los vértices de una de las representaciones que hace que se convierta en la otra.

Una transformación de los vértices 1,2,..,N es escoger una permutación de los números del 1 al N p1,p2,..,pN y renombrar el vértice i por pi .

Para ayudar a Fito implemente un algoritmo que lea dos representaciones de árboles y diga si son iguales.

Input

Entero 1<=N<=100000 que representa la cantidad de nodos de los dos árboles.

N líneas describiendo las aristas del primer árbol.

N líneas describiendo las aristas del segundo árbol.

En cada línea habrá dos enteros 1<=a,b<=N indicando que hay una arista entre el nodo a y el nodo b.

Output

“Si” si son iguales y “No” en caso contrario.

Sample test(s)

Hints

El ejemplo es el que se muetra en el enunciado del problema . Si se toma la permutación 2,3,1,5,4:

El vértice 1 se transforma en 2.

El vértice 2 se transforma en 3.

El vértice 3 se transforma en 1.

El vértice 4 se transforma en 5.

El vértice 5 se transforma en 4.