|
Matcom Online Grader
ℹ️ We've recently migrated MOG to a new server with a different grader. As a result, some features—especially those related to submission evaluation—might not work correctly. If you encounter any issues, please report them by clicking the exclamation icon in the bottom right corner of the website.
ACM 2014 - Round #2Ended |
G - Pie Problem V
Languages: C, C++, Java, Pascal, Haskell, Python, JavaScript, Tiger, C#
Time & Memory limits: (details)
Todo el mundo sabe cuál es el objetivo del tiro al blanco: disparar tan cerca del centro como sea posible. El centro de la diana coincide con el inicio de coordenadas $(0, 0)$. Considere $R$ como el radio del círculo más interior de la diana. El radio de un círculo externo tiene el doble del radio del círculo previo. Si un disparo es realizado fuera del ultimo círculo se obtendrán $0$ puntos.
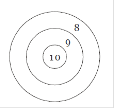La diana está compuesta de $10$ circunferencias cada una puntuando más a medida que se acerca al centro de la diana.
Si un disparo es realizado en el borde que limita dos circunferencias entonces puntuará como la más interna.
Input
Línea 1
: Dos enteros $R$ $(1 \leq R \leq 50)$ y $N$ $(1 \leq N \leq 150)$, el radio de la circunferencia más interna y la cantidad de tiros realizados.
Línea 2…N+1
: Dos enteros por línea $x_i$ y $y_i$ separados por espacio, representando el $i$-ésimo disparo $(-7000 \leq x_i, y_i \leq 7000)$.
Output
Línea 1 : Un solo entero, el total de puntos acumulados.
Sample test(s)
Input
1 2
1 1
0 0
Output
19
Hints
