Matcom Online Grader

En una placa de un circuito impreso, los alambres conductores están situados sobre una placa no conductora. Debido a que los conductores en una misma capa no se pueden cruzar sin crear un corto circuito, las placas con conductores están divididas en varias capas separadas por un material no conductor que es usado en los casos más complejos. No obstante, las placas con más capas son muy caras. Así, los fabricantes tratan de asignar los conductores requeridos a las places de tal manera que se minimice el número de capas necesarias. En esta tarea nosotros buscamos una placa donde cada conductor esté conectando dos puertos localizados en lados opuestos de la placa y trate de minimizar el costo de la placa.

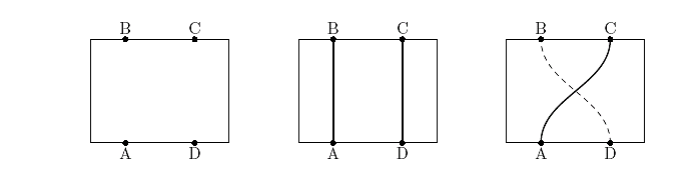
Considere, por ejemplo, la placa mostrada en la figura de abajo a la izquierda. Si un conductor tiene que conectar $A$ con $B$ y otro $D$ con $C$, esto puede ser logrado en una capa sencilla, como se muestra en la figura del centro. Pero un conductor conectando $A$ con $C$ y otro conectando $D$ con $B$ no pueden estar ubicados en la misma capa, como puede ser visto en la figura de la derecha.

Escriba un programa que dadas las localizaciones de los puntos extremos de los $N$ sobre una placa  $W \times H$  determine el número mínimo de capas necesarios para ubicar a todos los conductores. Se puede asumir que el ancho de los conductores es muy pequeño comparado a la distancia entre los puertos. Esto es, entre cualquier dos conductores, siempre hay suficiente espacio para un tercer conductor.

Input

Línea 1 : La primera línea contiene $N$ $(1 \le N \le 10^5)$, el número de conectores.
Línea 2 ... N+1 : Cada una de las siguientes $N$ líneas contienen dos enteros, $X_{i1}$ y $X_{i2}$ $(0 \le X_{ij}\le 10^6)$, separados por un espacio, representando que el $i$-ésimo conductor conecta los puntos $(X_{i1}, 0)$ y $(X_{i2},H)$. Se puede asumir que todos los $2*N$ puntos extremos dados en la entrada son distintos.

Output

Línea 1 : La primera y única línea debe contener un entero simple, el número mínimo de capas necesarias para ubicar todos los conductores requeridos.

Sample test(s)