Matcom Online Grader

Bruce  tiene  $M$  muchachos.  Él  va  a  comprar  caramelos  para  su  día  de  fiestas  favorito.  Los caramelos son vendidos solamente en cajas con forma triangular.  La primera línea de la caja triangular contiene $1$ caramelo, la segunda línea – $2$ caramelos, la tercera línea – $3$ caramelos y así sucesivamente.  Cajas con cualquier número de  filas desde $1$ hasta $N$ están disponibles.

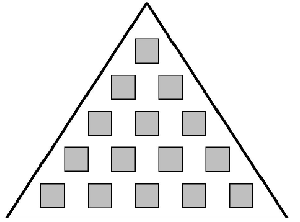
La figura del ejemplo muestra una caja con $5$ filas y $15$ caramelos.

Para  hacer  a los  niños  felices  Bruce  quiere  elegir  una  caja con  un  número  de  caramelos  que puedan ser igualmente divididos sin residuo entre los niños. Usted necesita contar cuántas elecciones apropiadas él tiene de todas las cajas disponibles.

Input

La primera línea de la entrada contiene dos enteros $N$ y $M$ $(1 \leq N, M \leq 2 \times 10^9)$.

$N$ – número máximo de filas en las cajas con forma de triángulo.
$M$ – número de muchachos que Bruce tiene.

Output

La primera y única línea de la salida contiene un entero – el número de diferentes tamaños de cajas apropiados de entre todas las cajas disponibles.

Sample test(s)