Matcom Online Grader

Fito desea comprar una moneda especial como un presente para su amigo. Fito vive en el pueblo $A$ y su amigo vive en el pueblo $B$. Existe un total de $N$ pueblos y $M$ caminos bidireccionales en su país.

Viajar por cada camino cuesta una cantidad de dinero. Fito conoce los precios y las localizaciones de los $K$ pueblos donde las monedas son vendidas. El  necesita  escoger  un  pueblo  para  comprar  la  moneda y un camino desde $A$ hasta  $B$ tal que minimice  el gasto total para viajar y el costo de comprar la moneda. Por ejemplo, si Fito va a comprar la moneda en el pueblo $Z$, entonces su costo es igual al costo de viajar desde $A$ hasta $Z$ más el costo de la moneda en $Z$ más el costo de viajar desde $Z$ hasta $B$.

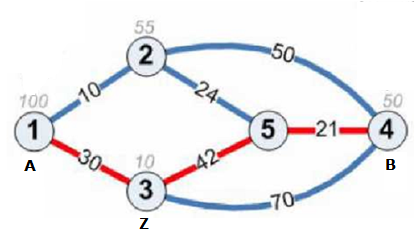
La  figura  presenta  un  ejemplo  del  mapa  de  caminos  con  una  óptima  ruta  resaltada  en  color  rojo ($Z = 3$).

Input

La primera línea de la entrada  estándar  contiene $3$ enteros:

$N$, $M$ y $K$ $(2 \leq N \leq 5000; 1 \leq M \leq 100000, 1 \leq K \leq N)$.

$N$ – número de pueblos en el país,

$M$ – número de caminos en el país,

$K$ – número de pueblos donde la moneda es vendida.

Todos los pueblos son numerados desde $1$ hasta $N$.

La segunda línea de la entrada estándar contiene $2$ enteros:

$A$ $B$ ($1 \leq A, B \leq N$; $A$ diferente de $B$).

$A$ – el índice del pueblo de Fito,

$B$ – el índice del pueblo de su amigo.

La tercera línea contiene $K$ pares de enteros:

$V_i$ $C_i$ $(1 \leq V_i \leq N, 1 \leq C_i \leq 10^9)$

$V_i$ – el índice del pueblo donde Fito puede  encontrar la moneda.

$C_i$ – el costo de la moneda en ese pueblo.

Todos los $V_i$ son diferentes.

Cada una de las siguientes $M$ líneas contienen $3$ números:

$X_i$ $Y_i S_i$ ($1 \leq X_i, Y_i \leq N$; $X_i$ diferente de $Y_i$; $1 \leq S_i \leq 10^5$)

$X_i$ $Y_i$ – los índices de los pueblos conectados por un camino bidireccional,

$S_i$ – el costo de viajar a lo largo del camino,

No dos pueblos son conectados por varios caminos.

Output

La  primera y única  línea de  la salida  estándar debe contener el gasto mínimo  posible. Se garantiza que la solución existe.

Sample test(s)