Matcom Online Grader

Un árbol binario de búsqueda (ABB) es un árbol donde cada nodo tiene a lo sumo dos hijos y a cada nodo x le es asociado un valor o clave (denotado por $k[x]$) tal que se cumple lo siguiente:

• Si un nodo $y$ pertenece al subárbol izquierdo de $x$, entonces $k[y] \le k[x]$.
• Si un nodo $y$ pertenece al subárbol derecho de $x$, entonces $k[x] \lt k[y]$.

Nosotros estamos diseñando el nuevo traductor que desplazará definitivamente a Babylon . Para cada ocurrencia de cada palabra en español en el texto, necesitamos buscar su equivalente en inglés. Una forma de realizar estas búsquedas es construir un ABB con las $N$ $(1 \le N \le 1000)$ palabras en español como claves. Para que el traductor sea un éxito, es necesario minimizar el tiempo total de búsqueda.

Más formalmente, dada una secuencia $K = (k_1, k_2, \dotsc, k_N)$ de $N$ claves diferentes ordenadas ascendentemente $(k_1 \lt k_2 \lt \dotso \lt k_N)$ y otra secuencia $P = (p_1, p_2, \dotsc, p_N)$, donde $p_i$ representa un valor similar a la probabilidad de que ocurra una búsqueda de la clave $k_i$ , nosotros necesitamos encontrar el ABB de costo mínimo para estas claves.

El costo del ABB se define como: $\displaystyle\sum_{i=1}^{N}{e_i p_i}$ donde $e_i$ representa el número de aristas entre el nodo $i$ y la raíz del árbol.

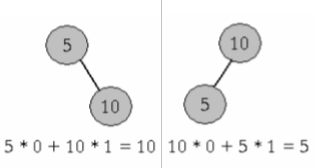
Dos árboles construidos a partir de las mismas claves. En cada nodo está indicada la probabilidad de ocurra una búsqueda de la clave correspondiente.

Input

En la primera línea estará escrito un número $N$, la cantidad de claves. En cada una de la próximas $N$ líneas aparecerá un entero $p_i$ $(1 \le p_i \le 1000)$, que representa la probabilidad de que ocurra una búsqueda de la clave $k_i$. Recuerde que, aunque no se muestren, $k_1 \lt k_2 \lt \dotso \lt k_N$.

Output

Un entero que representa el costo mínimo de construir el ABB con las probabilidades dadas.

Sample test(s)