MOG Round #26Ended |
C - Puntos alcanzables
Languages: C, C++, Java, JavaScript, Tiger, Python, Haskell, Pascal, C#
Time & Memory limits: (details)
Recientemente BitZero y BitOne descubrieron que $0^n = 0$ y $1^n = 1$ para cualquier $n \gt 0$, lo que les da el poder de viajar en distintas dimensiones, y esto los ha motivado mucho. Como el último juego no resultó como esperaban, deciden reintentarlo pero en dos dimensiones. Esta vez BitZero se coloca en el punto $(0, 0)$ con su lista de saltos en la mano. BitOne se coloca junto a él en el instante inicial y por cada número $X$ en la lista de BitZero, BitOne escoge una dirección y da un salto de longitud $X$. Esta vez nuestros amigos se preguntan si BitOne puede alcanzar un punto determinado dando
todos
los saltos que le indica BitZero.
Input
1ra línea
: tres enteros $N$ $(1 \le N \le 50)$, $X$ e $Y$ $(-1000 \le X, Y \le 1000)$ que representan la cantidad de saltos y las coordenadas del punto a alcanzar respectivamente.
2da línea : $N$ enteros positivos menores que 1000 indicando la longitud de cada salto.
2da línea : $N$ enteros positivos menores que 1000 indicando la longitud de cada salto.
Output
1ra línea
: La cadena "SI" (sin las comillas) cuando el punto $(X, Y)$ es alcanzable por BitOne, y "NO" (sin las comillas) cuando no es alcanzable.
Sample test(s)
Input
2 2 1
2 1
Output
SI
Input
2 2 2
2 1
Output
SI
Input
2 1 0
3 1
Output
NO
Notes
Hint
En el primer ejemplo, BitOne puede saltar hacia $(2, 0)$ y luego hacia $(2, 1)$.
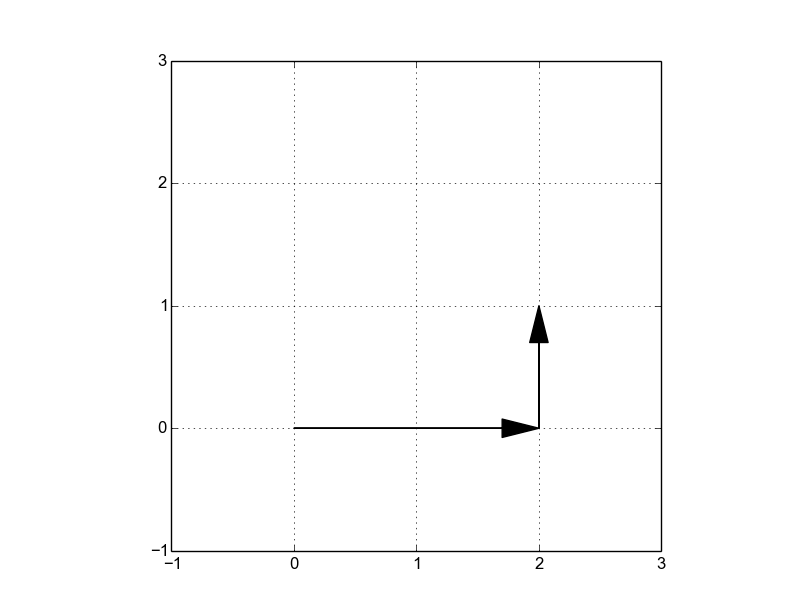
En el segundo ejemplo, BitOne puede saltar hacia $(\frac{22+2\sqrt{7}}{16}, \frac{22-2\sqrt{7}}{16})$ y luego hacia $(2, 2)$.

En el tercer ejemplo, BitZero se pone triste porque BitOne no puede llegar a $(1, 0)$.


