Matcom Online Grader

En teoría de grafos, un conjunto independiente es un conjunto de vértices del grafo tal que ninguno es adyacente a otro. Dado un grafo no dirigido $G=<V,E>$, encuentre, de ser posible, un conjunto independiente que tenga tamaño al menos $\displaystyle\sum_{i=1}^{N}{\frac{1}{d_i+1}}$, donde $d_i$ es el grado del $i$-ésimo vértice.

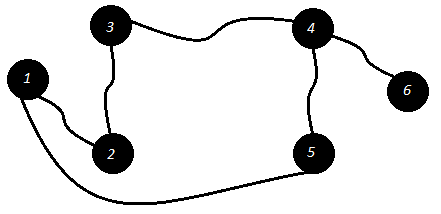En el grafo anterior tenemos que $V = \{1, 2, 3, 4, 5, 6\}$, $E = \{(1, 2), (1, 5), (2, 3), (3, 4), (4, 5), (4, 6)\}$ y $d_{1}=2$, $d_{2}=2$, $d_{3}=2$, $d_{4}=3$, $d_{5}=2$ y $d_{6}=1$. Por lo tanto queremos encontrar un conjunto independiente con tamaño al menos $\frac{1}{2+1}+\frac{1}{2+1}+\frac{1}{2+1}+\frac{1}{3+1}+\frac{1}{2+1}+\frac{1}{1+1}=\frac{25}{12}$ vértices. Una posible solución estaría compuesta por los vértices ${1, 3, 6}$.

Input

Línea 1 : Dos enteros $V$ y $E$ $(1 \le V \le 10^5, 1 \le E \le 10^5)$ separados por un espacio representando la cantidad de vértices y aristas en el grafo.
Línea 2…E+1 : Dos enteros diferentes separados por espacio $a$ y $b$ $(1 \le a, b \le V)$, indicando la existencia de una arista comunicando los vértices $a$ y $b$.

Output

Línea 1 : Si no existe solución, imprima “NO”. Si existe solución, escriba en la primera línea la cantidad $K$ de vértices del conjunto independiente encontrado, que cumple la condici ón dada.
Línea 2 : Si existe solución, la segunda línea debe contener $K$ enteros diferentes separados por espacio representando los vértices en dicha solución.

Sample test(s)