Matcom Online Grader

Isla Bella tiene hermosas playas que la rodean y muchos turistas ponen en mira dichos destinos. La compañía BrownSand se ha enfocado en la construcción de una nueva playa en la parte norte de Isla Bella. El terreno escogido presenta muchas irregularidades, formadas principalmente por zonas continuas por encima o debajo del nivel del mar. El terreno se puede describir como una secuencia de alturas donde un valor positivo corresponde a una zona elevada y uno negativo a un hueco. Un posible escenario sería:

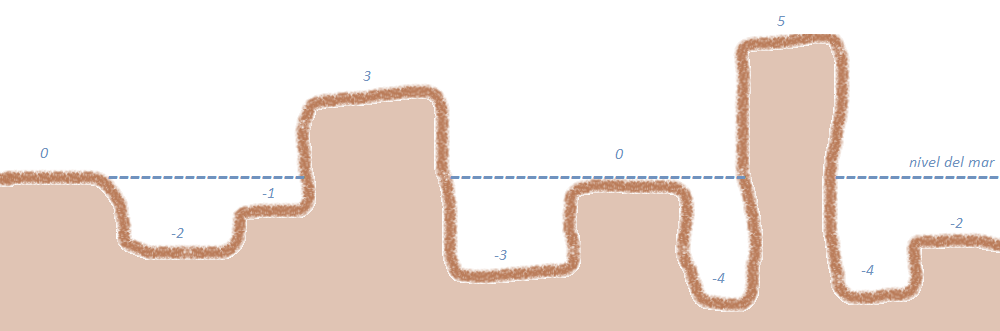
La imagen anterior describe las siguientes 10 zonas [0, -2, -1, 3, -3, 0, -4, 5, -4, -2]. El proyecto de construcción de la playa consiste en escoger un segmento continuo (de al menos una zona) y aplanarlo, es decir, llevarlo al nivel del mar poniendo o quitando arena como se necesite. La forma de ejecución de la obra consiste en dos tareas como sigue (una vez determinado el segmento):

1. La arena de las elevaciones (del segmento) se utiliza para llenar los huecos (del segmento).
2. Si sobra arena se saca el excedente del segmento. Puede ser que falte arena, en dicho caso se manda a buscar a otros lugares (siempre existe la cantidad necesaria).

El problema es que los trabajadores de la segunda fase solamente fueron contratados para eliminar o agregar exactamente $K$ unidades de arena, de esta forma, BrownSand quiere encontrar un segmento donde haya que eliminar o agregar $C$ unidades de arena, y $C$ esté lo más cerca posible de $K$, es decir, que se minimice $|C - K|$.

Input

Línea 1 : Dos enteros $N$ y $K$ $(1 \le N \le 10^5, 1 \le K \le 10^{14})$, la cantidad de zonas en el terreno escogido y las unidades de arena en el contrato de los trabajadores de la segunda tarea.
Línea 2 : N enteros separados por espacio $h_1, h_2, …, h_n$ $(-10^9≤ hi ≤ 10^9)$, las alturas de las zonas en el terreno.

Output

Línea 1 : Dos enteros separados por espacio $S$ y $E$ $(1 \le S \le E \le N)$, el inicio y final del segmento seleccionado respectivamente. Si existen múltiples soluciones, imprima cualquiera.

Sample test(s)

Hints

Hint

Primer Ejemplo

Si se escoge el segmento [5, 10] entonces en la primera fase se utilizan las 5 unidades de arena de la octava zona para rellenar las otras, luego los trabajadores de la segunda tarea tienen que buscar C = 8 unidades de arena para terminar de aplanar.

Segundo Ejemplo:

El mejor segmento consiste solamente de la cuarta zona, donde hay que buscar $C = 5$ unidades de arena, minimizando el exceso ($= |4-5| = 1$).