Matcom Online Grader

Isla Bella está compuesta de $N$ provincias numeradas de $1$ a $N$. La provincia con número $1$ es la capital. Las provincias están conectadas por $N-1$ carreteras bidireccionales, cada una con una longitud expresada en kilómetros. Hay solo una forma de viajar entre cualquier par de provincias sin repetir (es decir, el grafo de caminos es un árbol).

Todas las provincias tienen solamente una terminal de transporte. Cada terminal está caracterizada por el tiempo de preparar un ómnibus para un viaje y la velocidad constante que deben mantener sus choferes (expresada en kilómetros por minuto) después de la partida. Todos los viajes tienen como destino la capital y se realizarán por el único camino más corto.

Una vez montado en un ómnibus, el chofer no permitirá que nadie se baje, excepto cuando arriben a una provincia. En dicho caso, las personas pueden optar por hacer un cambio y esperar por un ómnibus en la terminal de dicha provincia.

Input

Línea 1 : Un entero $N$ $(1 \le N \le 100000)$, el número de provincias de Isla Bella.

Línea 2…N : Tres enteros separados por espacio $u$, $v$, $d$ $(1 \le d \le 10000, 1 \le u, v \le N)$ indicando que existe un camino de longitud $d$ kilómetros conectando las provincias $u$ y $v$.

Línea N+1..2*N-1 : Dos enteros separados por espacio $S$, $V$ $(0 \le S \le 10^9, 1 \le V \le 10^9)$ representando el tiempo de preparación de un viaje y la velocidad constante de un ómnibus en cada provincia respectivamente. (La i-ésima línea contendrá la información de la terminal con número $i – N + 1$).

Output

Línea 1 : $N-1$ enteros separados por espacio. El i-ésimo entero es el menor tiempo necesario para viajar desde la provincia $i+1$ hasta la capital.

Sample test(s)

Hints

Hint
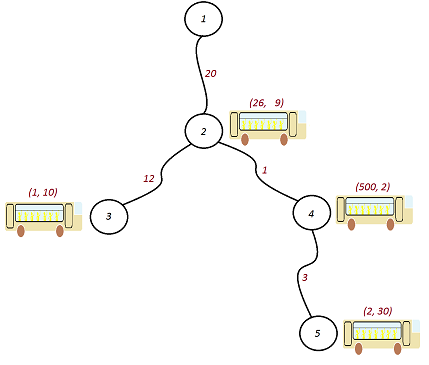
Los caminos y las longitudes se muestran en la imagen de abajo. El tiempo de preparación y velocidad de un ómnibus en cada provincia están escrito entre paréntesis $(S, V)$. El mínimo tiempo de viajar desde la provincia 5 hasta la capital se obtiene como sigue: Se coge un ómnibus en la terminal de la provincia 5, se espera 2 minutos hasta que esté listo el viaje. Se viaja hasta la ciudad 2, ubicada a 4 kilómetros en un tiempo de 120 minutos. Se hace un cambio de ómnibus en la terminal de la provincia 2. Se esperan 26 minutos y luego se recorren los restantes 20 kilómetros en 180 minutos. El tiempo total es 2 + 120 + 26 + 180 = 328.