Matcom Online Grader
Faculty of Mathematics and Computer Science of University of Havana

Los habitantes de la galaxia Messier 83 tienen un sistema peculiar de autopistas formada por carreteras en forma de circunferencia. Estas carreteras llamadas anillos son esenciales durante el recorrido de un punto a otro de la galaxia. Luego de viajar un rato por un anillo, el paisaje se vuelve monótono y se puede alternar a través de los puntos de cambios . Un punto de cambio no es más que una localización donde dos anillos se intersectan.

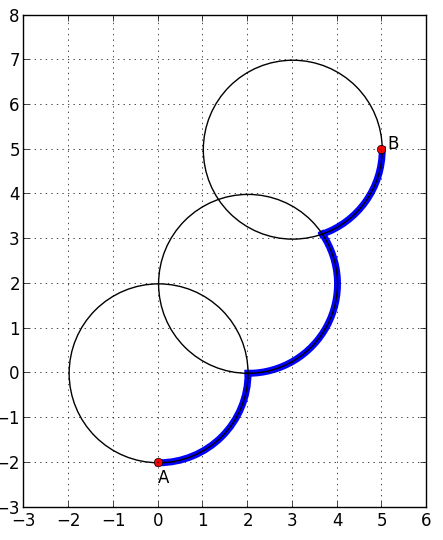
Como programador ágil y certero, el presidente de Messier 83 lo ha contratado para implementar un software de estimación de distancia. Es decir, dado la distribución de los anillos, un punto inicial $A$ y otro final $B$, usted debe determinar cuál es la menor distancia que se debe recorrer para ir de $A$ hasta $B$ pasando solamente por el borde de los anillos.

Input

Línea 1 : Un entero $N$ $(1 \le N \le 500)$, la cantidad de anillos en Messier 83 .
Línea 2 : Cuatro enteros $A_x$, $A_y$, $B_x$, $B_y$ $(-10^6 \le A_x, A_y, B_x, B_y \le 10^6)$ representado la posición inicial $(A_x, A_y)$ y la final respectivamente $(B_x, B_y)$.
Línea 3 … N+2 : Tres enteros separados por espacio $X$, $Y$, $R$ $(-10^6 \le X, Y \le 10^6, 1 \le R \le 10^6)$. Donde $X$ e $Y$ representan el centro del anillo y $R$ su radio.
nota : Los puntos $A$ y $B$ se encontrarán siempre sobre el borde de algún anillo.

Output

Línea 1 : La menor distancia de viajar desde $A$ hasta $B$. El valor absoluto de la diferencia entre la solución oficial y su respuesta no debe ser mayor que $10^{-4}$. Si no hay solución imprima $-1$.

Sample test(s)

Hints

Hint
Este es el recorrido óptimo para el ejemplo: