Matcom Online Grader

Considerando las habilidades de Fito en computación, el alcalde de Isla Grande le propuso la siguiente tarea: dada la información de las carreteras que unen ciudades en Isla Grande y sus longitudes, Fito debe calcular la menor distancia de ir de una ciudad $s$ a otra $t$. Luego de aceptar la oferta, Fito recibió $E+1$ correos del alcalde. En el primer correo se envió la cantidad de ciudades $V$ en Isla Grande, la cantidad de carreteras $E$ y la identificación de $s$ y $t$ respectivamente. Los subsiguientes $E$ correos enviados por el alcalde, contenían la identificación de un par de ciudades $a$ y $b$ conectadas por una carretera de longitud $l$. Fito conoce lo poco relacionado que está el alcalde con las nuevas tecnologías y viendo en retrospectiva el asunto desea conocer cuál hubiese sido la menor cantidad de mensajes que debía recibir para realizar su tarea correctamente.

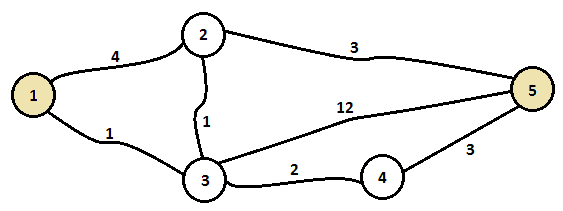
Por ejemplo, considere que Isla Grande tiene $V=5$ ciudades unidas por $E=7$ carreteras y que el alcalde desea conocer la menor distancia entre las ciudades $1$ y $5$. Para esto, Fito recibe los siguientes correos:

- 1er correo: $V=5$, $E=7$, $s=1$, $t=5$.
- 2do correo: $a=1$, $b=2$, $l=4$.
- 3er correo: $a=2$, $b=5$, $l=3$.
- 4to correo: $a=1$, $b=3$, $l=1$.
- 5to correo: $a=3$, $b=4$, $l=2$.
- 6to correo: $a=2$, $b=3$, $l=1$.
- 7mo correo: $a=3$, $b=5$, $l=12$.
- 8vo correo: $a=4$, $b=5$, $l=3$.

Fito puede determinar que la menor distancia de $1$ a $5$ es $5$ utilizando el camino $\{1,3,2,5\}$. De esta manera, solamente era necesario recibir los primeros $6$ correos.

Input

Línea 1 : Cuatro enteros separados por espacio $V$, $E$ $(1 \le V, E \le 2*10^5)$, $s$ y $t$ $(1 \le s,t \le V)$.
Línea 2…E+1 : La $i$-ésima línea $(2 \le i \le E+1)$ contendrá la información recibida en el $i$-ésimo correo: tres enteros separados por espacio $a$, $b$ y $l$ $(1 \le a \ne b \le V, 1 \le l \le 10^6)$ representando que las ciudades $a$ y $b$ están conectadas por una carretera de longitud $l$.

Output

Línea 1 : Dos enteros separados por espacio $k$ y $d$, donde $k$ es la cantidad necesaria de correos a recibir para determinar la menor distancia $d$ entre $s$ y $t$. Note que los correos se deben recibir en orden. Se asegura que entre $s$ y $t$ existe al menos un camino.

Sample test(s)

Hints

Hints