Matcom Online Grader

Durante el fin de semana Fito debe pintar la pared lateral de su casa. Él ya creó un plan para realizar dicha tarea: Fito asume que la pared es un rectángulo de dimensiones $H \times W$ en donde pintará $N$ rectángulos de diferentes colores. Luego de pensar un poco, Fito nota que puede ahorrar pintura si se imagina el resultado final de su obra maestra.

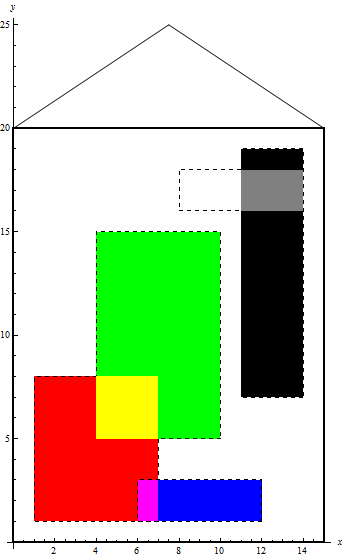En la figura anterior $H=20$, $W=15$ y Fito considera pintar los siguientes rectángulos:
- Rectangle[{1, 1}, {7,8}] Red
- Rectangle[{4, 5}, {10,15}] Green
- Rectangle[{6, 1}, {12, 3}] Blue
- Rectangle[{11, 7}, {14, 19}] Black
- Rectangle[{8, 16}, {14, 18}] White

Como observamos en la figura:
- El rectángulo verde fue pintado sobre el rojo y la intersección se  tornó amarilla.
- El rectángulo azul fue pintado sobre el rojo y la intersección se  tornó magenta.
- El rectángulo blanco fue pintado sobre el negro y la intersección se  tornó gris.

Fito quiere saber cuáles serán los colores resultantes y la cantidad de unidades cuadradas que ocupará cada uno luego de pintar los $N$ rectángulos. Adicionalmente él cuenta con una lista de transformación de la forma $[(A_1,B_1,C_1 ),(A_2,B_2,C_2 ),…,(A_T,B_T,C_T)]$ donde $(A_i,B_i,C_i)$ indica que si los colores $A_i$ y $B_i$ se mezclan el resultado es el color $C_i$. Conocemos que el color de la pared no afecta los colores pintados sobre esta y si la mezcla de dos colores no aparece en la lista de transformación de Fito, entonces el color resultante es el último que se aplique.

Input

Línea 1 : Dos enteros separados por un espacio $H$ y $W$ $(1 \le H,W \le 10^9)$ representando la altura y el ancho de la pared lateral de la casa de Fito respectivamente.
Línea 2 : Un entero $N$ $(1 \le N \le 300)$, la cantidad de rectángulos que Fito desea pintar sobre la pared.
Línea 3 … N+2 : Cuatro enteros $X_{lo}$,$Y_{lo}$,$X_{hi}$,$Y_{hi}$ $(0 \le X_{lo} \lt X_{hi} \le W,0 \le Y_{lo} \lt Y_{hi} \le H)$ y el color $C$ separados por espacio. Donde $(X_{lo},Y_{lo})$ representa el punto de la esquina inferior izquierda del rectángulo y $(X_{hi},Y_{hi})$ la equina superior derecha. El color $C$ es una cadena de caracteres del alfabeto inglés en minúscula de longitud a lo sumo $20$.
Línea N+3 : Un entero $T$ $(0 \le T \le 1000)$ la cantidad de mezclas en la lista de transformaciones de Fito.
Línea N+4…N+T+3 : Tres cadenas por línea separadas por espacio $A_i$,$B_i$,$C_i$ indicando que la mezcla de los colores  $A_i$ y $B_i$ resultan en  $C_i$ $(A_i \ne B_i)$. No habrán dos mezclas iguales produciendo colores diferentes.

Output

Línea 1 … : Por cada color presente en la pared imprimir el nombre y la cantidad de unidades cuadradas separados por espacio. Ubicar primero aquellos colores que su nombre sea menor lexicográficamente.

Sample test(s)