Matcom Online Grader

El Judo es uno de los estilos principales de la lucha deportiva más practicados hoy en día en todo el mundo. La UNESCO declaró el judo como el mejor deporte inicial formativo para niños y jóvenes de 4 a 21 años, ya que permite una educación física integral.

Muchos estudios han demostrado los beneficios de la práctica del judo especialmente en niños hiperactivos, como es el caso de Fito. Es por esto que sus padres decidieron apuntarlo en clases de Judo y recientemente compitió en un torneo.

En el torneo participaron $2^n$ judocas numerados de $1$ a $2^n$. En la primera ronda se hicieron $2^{n-1}$ combates entre los judocas $1$ y $2$, $3$ y $4$, ..., $2^n - 1$ y $2^n$, y los perdedores se retiraron del torneo. En la segunda ronda se hicieron $2^{n-2}$ combates con los restantes $2^{n-1}$ competidores, entre los ganadores del primero y el segundo, los ganadores del tercero y el cuarto, y así sucesivamente. Las demás rondas se hicieron de forma similar y el ganador del juego de la última fue considerado el ganador del torneo. En la figura a continuación se muestra el organigrama del primer caso de ejemplo.

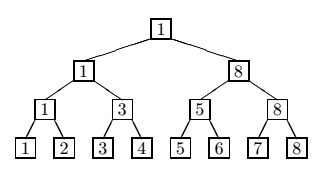
La duda que tiene Fito está relacionada con el ranking final y el orden relativo de los competidores. No hay ninguna duda sobre el primer lugar (el ganador de la última ronda ), pero es un poco difícil definir los otros lugares. Un orden relativo es válido si no existe una contradicción, o sea, si no hay un jugador mejor ubicado que otro que lo derrotó a él. Además hay que tener en cuenta la transitividad, esto significa que si un competidor $A$ le ganó a otro $B$ y este le ganó a $C$, entonces se asume que $A$ le ganó a $C$.

Fito quiere saber para determinados competidores cuál puede ser el mejor lugar que puede reclamar en el ranking y el peor que le pueden asignar. Por ejemplo, un judoca que perdió con el que resultó campeón pudiera reclamar el 2do lugar.

Input

La entrada va a contener varios casos de prueba ( a lo sumo 20 ). Cada uno estará compuesto por tres líneas: La primera de ellas va a tener un entero $N$ $(1 \le N \le 8)$ indicando que habrá $2^N$ competidores. La segunda línea va a contener los ganadores de cada uno de los combates en el orden en que se van celebrando en el organigrama de izquierda a derecha. La tercera línea tendrá un entero $M$ y seguidamente $M$ enteros $k_1, k_2,…, k_M$ que son los números correspondientes a los competidores en que Fito está interesado.

Output

Para cada $k_i$ se debe imprimir la línea “ Player $k_i$ can be ranked as high as $h$ or as low as $l$. ”, sin las comillas y en el mismo orden que aparecieron los $k_i$ en la entrada. Las salidas correspondientes a casos de prueba distintos deben estar separadas por una línea en blanco.

Sample test(s)