Matcom Online Grader

Algo muy común en la electrónica es saber hasta qué punto se pueden unir dos circuitos integrados. Fito está ahora trabajando para Intel y le han dado la tarea de calcular, dado un filamento de ciertas aleaciones de cobre que se calienta $n$ grados, cuánto es que se expande. Esta fórmula es conocida: $N_L = (1 + n * C) * L$ , siendo $N_L$ la nueva longitud del filamento, $n$ la cantidad de grados a los que se calienta el filamento, $C$ es el coeficiente de expansión de la aleación de cobre y $L$ es la longitud original del filamento.

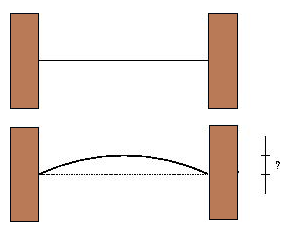
Este filamento es montado sobre dos bases de un aislante y al dársele calor, el filamento se expande formando un arco de una circunferencia.  Su tarea es calcular la distancia que se desplazó del centro del filamento.

Input

Cada entrada posee múltiples casos de prueba.  Cada caso de prueba contiene tres números  reales positivos separados por un espacio, el primero es la distancia inicial del filamento en milímetros, la temperatura en grados y el coeficiente de expansión de la aleación de prueba. Siempre se garantiza que el filamento no se expande más de la mitad de su longitud inicial. La última línea de la entrada son tres números negativos, estos no deben de ser procesados.

Output

Por cada caso de prueba de la entrada se debe de imprimir el desplazamiento del centro del filamento en milímetros con tres cifras de precisión.

Sample test(s)