|
Matcom Online Grader
ℹ️ We've recently migrated MOG to a new server with a different grader. As a result, some features—especially those related to submission evaluation—might not work correctly. If you encounter any issues, please report them by clicking the exclamation icon in the bottom right corner of the website.
III Copa UHEnded |
Este año ha sido bueno para Fito, logró aprobar el 2do año de su carrera y con muy buenos resultados. Pero para entrenar para los concursos de ACM debe esforzarse más, así que decide combinar los conocimientos aprendidos en un ejercicio muy interesante que involucra a grafos no dirigidos, árboles abarcadores y números de Fibonacci.
El ejercicio en cuestión es el siguiente: dado un grafo no dirigido y conexo, donde cada arista tiene un color (blanco o negro), determinar si existe un árbol abarcador de dicho grafo tal que la cantidad de aristas negras que contiene es un número de Fibonacci.
El ejercicio en cuestión es el siguiente: dado un grafo no dirigido y conexo, donde cada arista tiene un color (blanco o negro), determinar si existe un árbol abarcador de dicho grafo tal que la cantidad de aristas negras que contiene es un número de Fibonacci.
Input
En la primera línea
: dos números enteros $N$ y $M$ $(1 \le N \le 10^5, N-1 \le M \le 10^5)$ que representan la cantidad de nodos y de aristas del grafo, respectivamente.
En las próximas N líneas : tres enteros $A$, $B$ y $C$ $(1 \le A, B \le N)$ en cada línea, que indican que existe una arista en el grafo entre los vértices $A$ y $B$ con color $C$. Los colores blanco y negro serán representados por los valores $0$ y $1$ respectivamente.
Se garantiza que el grafo dado es conexo.
En las próximas N líneas : tres enteros $A$, $B$ y $C$ $(1 \le A, B \le N)$ en cada línea, que indican que existe una arista en el grafo entre los vértices $A$ y $B$ con color $C$. Los colores blanco y negro serán representados por los valores $0$ y $1$ respectivamente.
Se garantiza que el grafo dado es conexo.
Output
Si existe un árbol abarcador tal que la cantidad de aristas es un número de Fibonacci, la respuesta debe ser "Si" (sin las comillas), en caso contrario, "No" (sin las comillas).
Sample test(s)
Input
5 5
1 2 1
2 3 1
3 4 1
4 5 1
5 1 1
Output
No
Input
5 5
1 2 1
2 3 1
3 4 0
4 5 1
5 1 1
Output
Si
Hints
Los números de Fibonacci son aquellos que pertenecen a la secuencia $F_n = \begin{cases} 1 \qquad \qquad \qquad n < 2 \\ F_{n-1} + F_{n-2} \quad n \ge 2 \end{cases}$
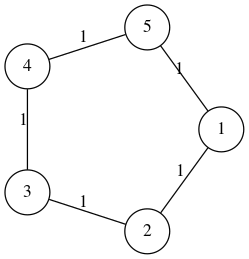
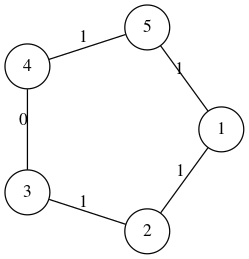
Estos son los grafos de los 2 casos de ejemplo, respectivamente. En el segundo caso, es posible encontrar un árbol abarcador con exactamente 3 aristas negras.
