Matcom Online Grader
Faculty of Mathematics and Computer Science of University of Havana

Los números de Fibonacci tienen la siguiente forma:

F ₁ = 1,

F ₂ = 2,

F _i = F _{i - 1} + F _{i - 2} , i > 2.

Considetemos un conjunto no vacío S = { s ₁ , s ₂ , ..., s _k }, donde cada elemento es un número de Fibonacci. Hallemos la suma de los valores del conjunto de elementos:

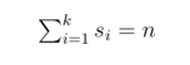
Llamamos al conjunto S una descomposición del número N en suma de números de Fibonacci. Es fácil de ver que existen números con varias descomposiciones en sumas de Fibonacci. Por ejemplo, el 13 tiene 13, 5 + 8, 2 + 3 + 8; dando tres descomposiciones. El 16 tiene: 3 + 13, 1 + 2 + 13, 3 + 5 + 8, 1 + 2 + 5 + 8; dando cuatro descomposiciones. Dado un número n, determine el número de posibles descomposiciones en suma de números de Fibonacci.

Input

La primera línea contiene un entero t — la cantidad de casos (1 ≤ t ≤ 10 ⁵ ). Cada una de las siguientes t líneas contiene un caso. Cada caso es un entero n (1 ≤ n ≤ 10 ¹⁸ ).

Output

Para cada caso imprima una línea con un número que será la respuesta al problema.

Sample test(s)

Hints

Dos descomposiciones son diferentes si existe un número que está contenido en la primera pero no en la segunda. Dos descomposiciones que difieren en el orden de los sumandos son iguales.