Matcom Online Grader

1ra Copa MATCOM - soluciones by leandro 9 years, 10 months ago

Problema A: Autofoto
Sea $L[i]$ el mayor índice menor estricto que $i$ tal que $A[L[i]] = A[i]$. Si no existe tal $L[i]$ entonces $L[i] = 0$.

Para cada intervalo $[a,b]$ buscamos el mayor valor de $L$ en ese rango, definámoslo como $L_{(a,b)}$. Esto lo podemos hacer con un RMQ o una estructura de datos en $O(lgN)$ por cada query.  Luego, en un rango $[a, b]$ existe al menos un elemento repetido si y solo si $a \le L_{(a,b)}$.

Problema B: Beyonce en la Habana
Podemos resolver este ejercicio usando el algoritmo de Dijkstra para hallar camino mínimo. La modificación aquí es a la hora de hacer RELAX en una arista $u-v$, si Beyonce estuvo “usando” esta arista en el intervalo de tiempo $[a,a + 1,…,b]$ pueden suceder dos casos:

Caso 1 : $D[u] \lt a$ o $D[u] \gt b$, en este caso se hace RELAX normalmente, es decir $D[v] = min(D[v],D[u] + w(u,v))$
Caso 2 : $a \le D[u]$ y $D[u] \le b$, en este caso esperamos a que Beyonce termine de cruzar por la arista y entonces hacemos RELAX, es decir $D[v] = min(D[v],b + w(u,v))$.

Problema C: Caramelos de Fito
Sea $F(W, H)$ el número de formas de vaciar el paquete si existen $W$ caramelos enteros y $H$ mitades. La recurrencia quedaría:

$F(W,H) =
\begin{cases}
F(W-1, H+1) + F(W, H-1)       & \quad \text{Si } W \gt 0 \text{ y } H \gt 0\\
F(W-1, 1) & \quad \text{Si } W \gt 0\\
1 & \quad \text{e.o.c}
\end{cases}$

Problema D: Deportes en la Universidad

TODO : Demostración ...

Problema E: Encriptando listas
Sea $S=a_1+a_2+..+a_n$. Simulando el algoritmo cada fase del mismo quedaría como sigue:

Luego, si calculamos el valor de $P_T=(n-1)^{T-1}-(n-1)^{T-2}+⋯+(-1)^T$ podemos buscar la lista resultante de aplicar el algoritmo del problema en $O(N)$ iterando por cada $i$ $(1 \le i \le n)$.
Para calcular $P_T$ elevaremos la siguiente matriz a la $T$:

$\begin{bmatrix}n-1 & 1\\0 & -1\end{bmatrix}$

Notemos que $\begin{bmatrix}n-1 & 1\\0 & -1\end{bmatrix}^k = \begin{bmatrix}(n-1)^k & (n-1)^{k-1}-(n-1)^{k-2}+...+ (-1)^k\\0 & -1^k\end{bmatrix}^k$. Utilizando exponenciación rápida , calculamos $\begin{bmatrix}n-1 & 1\\0 & -1\end{bmatrix}^T$ en $O(lgT)$. El valor deseado $P_T$ será el valor de la matriz resultante de la primera fila y última columna $(1,2)$.

Problema F: Fracciones irreducibles
Buscamos el máximo común divisor $g$ de $a$ y $b$, la fracción reducida es $(\frac{a}{d}, \frac{b}{d})$.

Problema G: Gran subsecuencia
Buscamos la mayor letra, si está repetida entonces la que se encuentre más a la izquierda. La concatenamos al principio de nuestra solución (inicialmente vacía), ignoramos todos los caracteres a su izquierda y volvemos a repetir el proceso con la subcadena que se encuentra estrictamente a su derecha. Repetimos el proceso hasta que terminemos con la cadena vacía. Ejemplo:

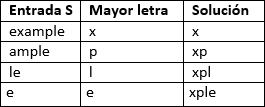
La solución sugiere $O(N^2)$ pero si calculamos $M[i]$ como la primera aparición de la mayor letra en la subcadena $S[i … N]$ en $O(N)$, entonces podemos construir la solución en $O(N)$.

Problema H: Hay caminos de amistad
En el grafo que se forma de unir los estudiantes por su relación de amistad, siempre existe un camino de Hamilton. Nuestra solución en $O(N^2)$:

Si existe algún error deje su comentario.