MOG Round #T4 - Sketches by leandro 12 years, 7 months ago
Buscamos y guardamos la posición del menor número en la secuencia, este es el puesto de Fito antes de ordenar la formación. Después, se ordena la secuencia.
Calculamos independientemente la cantidad de palíndromos par e impar con longitud menor igual que N.
Par
Sea P(x) la función que calcula la cantidad de palíndromos de longitud 2 * x, es fácil ver que P(x) = 26 x . Luego, la cantidad de palíndromos de longitud par de tamaño menor o igual que N es:
Impar
Similar, definimos I(x) la función que calcula la cantidad de palíndromos de longitud 2 * x + 1. I(x) = 26 x+1 La cantidad de palíndromos de longitud impar de tamaño menor o igual N que es:
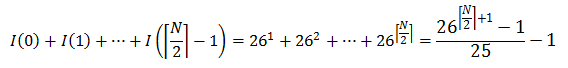
Para realizar los cálculos eficientemente debemos usar la función de exponenciación siguiente:

Para obtener el inverso de 25 modulo 1000000007 hacemos:
pow_mod (25, 1000000007 - 2, 1000000007)
Aplicamos camino mínimo desde A y B hacia todos los vértices del grafo. Buscamos la mejor solución de entre los K pueblos, es decir, minimizamos δ(A, k)+δ(B, k)+ C_k donde δ(u, w) es la distancia minima del pueblo u al pueblo w , y C_k es el costo de la moneda en el pueblo k .
Aplicamos programación dinámica en este ejercicio, dp[i][j][d] es lo mejor que podemos obtener hasta la i -esima fila, eligiendo el intervalo que empieza en j , con característica d .
La característica d dice el estado de la solución hasta el momento. Los estados son:
Estado 0 : Indica que el intervalo que comienza en j no se conecta con los intervalos en la solución óptima con ninguno de los tres bordes. En el ejemplo, los intervalos en azul y el rojo son candidatos a ser una solución de dp[6][1][0] , porque el intervalo rojo no se conecta a ninguno de los tres bordes señalados.
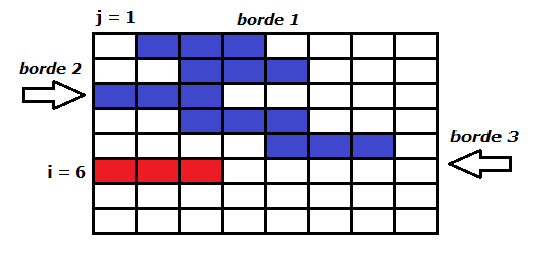
Estado 1 : El estado indica que el último intervalo se conecta solamente al borde 1.
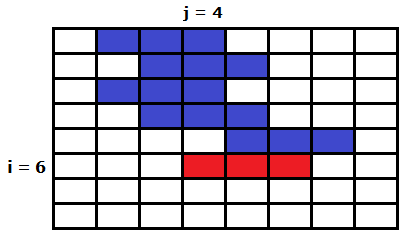
En el ejemplo, el intervalo rojo se conecta con el primer borde solamente.
De esta manera podemos ir formando los estados. Como máximo tenemos 8 estados, teniendo las combinaciones de los bordes. Se puede usar máscaras para guardar los estados. No obstante, hay combinaciones que son no validas, por ejemplo: no podemos conectar el borde 2 y el borde 3 porque los ratones cruzarían de un lado a otro (tampoco podemos conectar el borde 1 con la última fila):
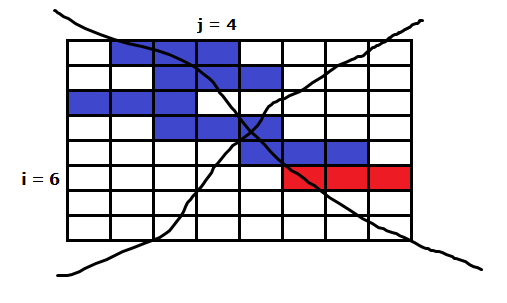
Para calcular un valor dp[i][j][d] debemos probar con todas las maneras de ubicar un intervalo en la fila anterior, nótese que el último intervalo en una solución solo se conecta a los bordes por el mismo o por un intervalo ubicado en la fila inmediata superior. Se pueden computar todos los estados en tiempo O(N 3 ) obviando la constante que es menor que 8.
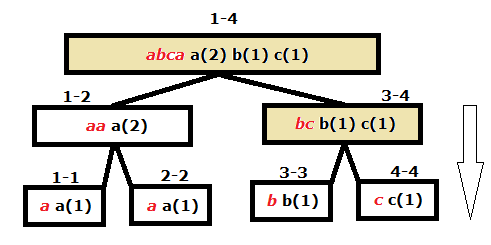
Para este ejercicio se puede utilizar un árbol de rango ( segment tree ). En cada nodo del árbol guardamos la cantidad de letras de cada tipo en ese rango. En el siguiente dibujo se muestra lo anterior:
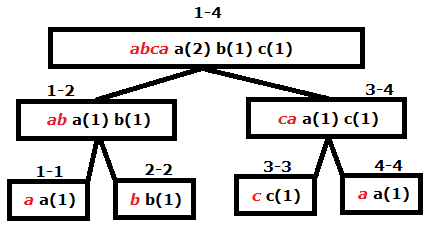
Nota: Las cadenas en rojo no se guardan realmente en los nodos, es para dar una idea.
Definimos la siguiente operación sobre el segment tree:
- Dado un intervalo [l, r] calcular cuántas letras de cada tipo hay en este intervalo.
Esta operación se puede hacer fácilmente “bajando” por el árbol y almacenando las letras de cada nodo. Esto se hace en O(25 * logN), logN para recorrer el árbol y 25 para recorrer las letras en los nodos del intervalo.
Cada vez que se ordenen los caracteres de un rango, hacemos la operación anterior y después distribuimos las letras en el árbol. Nótese que una vez aplicada la operación anterior obtenemos simplemente un arreglo de 26 enteros, donde la posición i-esima determina la cantidad de veces que aparece la letra i en [l, r].
En el dibujo supongamos que debemos ordenar los caracteres en [2, 4] los nodos visitados son los que están marcados:
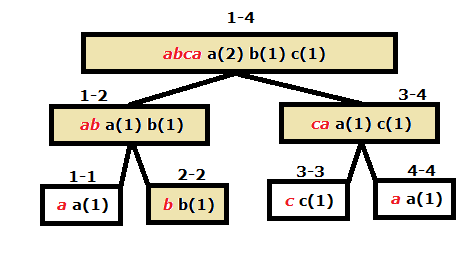
De aquí obtenemos a(1),b(1),c(1). Después tenemos que distribuir los tres caracteres en orden ascendente. Al nodo 2-2 le corresponde la letra a y al nodo 3-4 le corresponde las letras b y c. Después de distribuir los caracteres ordenados obtenemos el árbol siguiente.
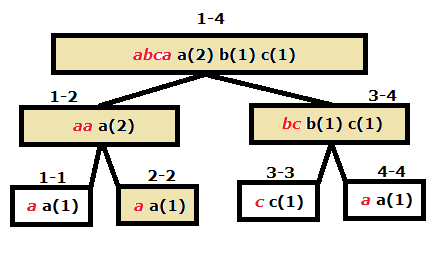
Ahora, tenemos en el nodo 1-4 que la cadena abca no aparece en efecto de esta manera, más bien aparece como aabc, pero esto no importa, de cierta manera los caracteres aparecen y son los mismos.
El nodo 1-2 se actualizó cuando se “subía” desde el nodo 2-2 . No obstante los nodos 3 -3 y 4 -4 no tienen los valores correctos. Para arreglar esto debemos llevar en cada nodo una marca que indique que el debe ser propagado cuando se visite ( Lazy Propagation ). De esta manera cuando se visite el nodo 3-4 habrá una marca que indique que deben propagarse los valores hacia los hijos.
Después de hacer todos los queries . Se recorre el árbol propagando hacia abajo los valores. Al final, la cadena queda en las hojas.
Ejercicios parecidos:


